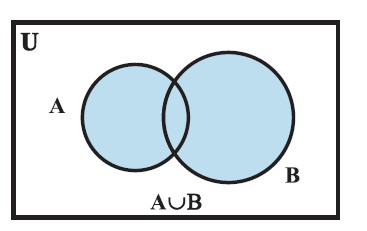
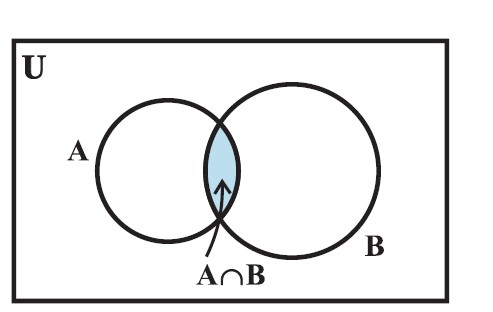
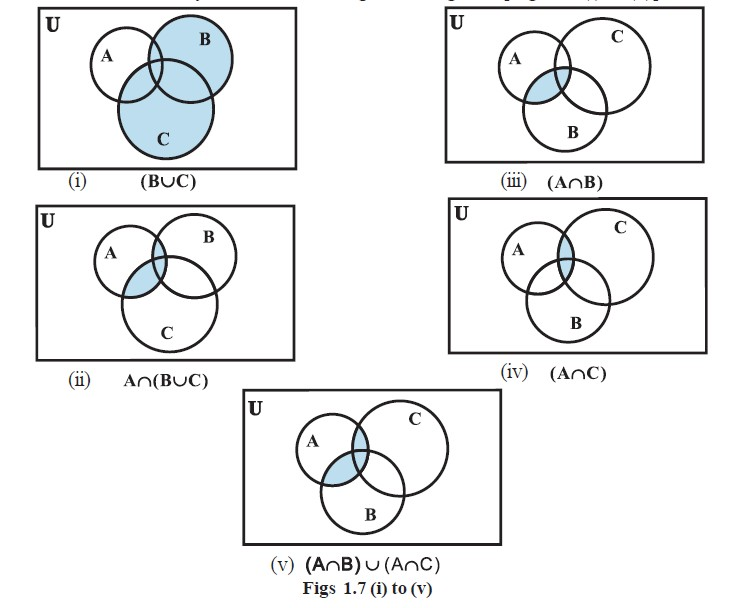
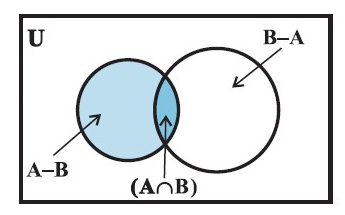
Mathematics Venn Diagrams, Union of sets, Intersection of sets, Difference of sets And Complement of a Set

Venn Diagrams :

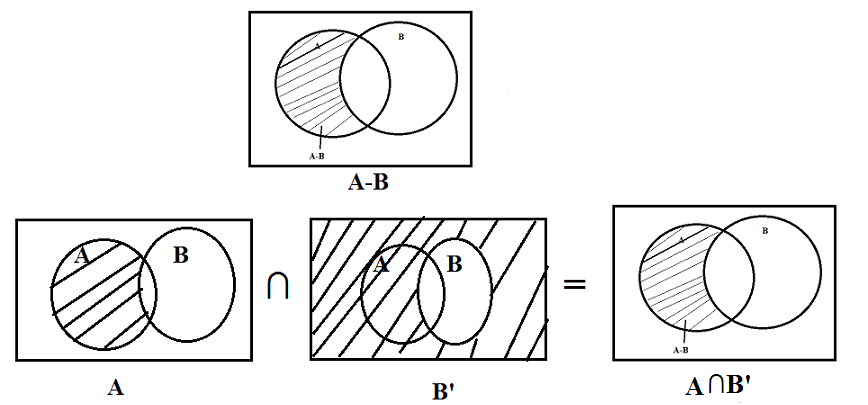
- A Venn diagram is a diagram that uses circles to illustrate the relationships among sets.
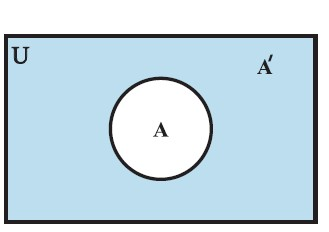
- These diagrams consist of rectangles and closed curves usually circles. The universal set is represented usually by a rectangle and its subsets by circles.

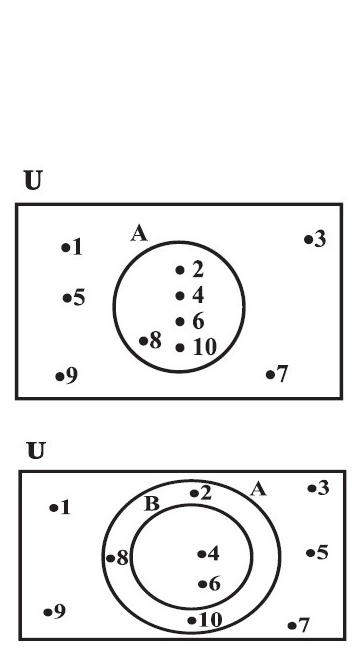
E.g. 1 : In Fiig. `U = {1,2,3, ..., 10}` is the universal set of which `A = {2,4,6,8,10}` is a subset.

E.g. 2 In Fig , `U = {1,2,3, ..., 10}` is the universal set of which

`A = {2,4,6,8,10}` and `B = {4, 6}` are subsets, and also `B ⊂ A.`

Operations on Sets :

Union of sets :

- The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both). The common elements being taken only once.
- Symbolically, we write `A ∪ B` and usually read as ‘A union B’.

`A ∪ B = { x : x ∈ A` or `x ∈B }`

Eg., Let `A = { 2, 4, 6, 8}` and `B = { 6, 8, 10, 12}`. Find `A ∪ B`.

`A ∪ B = { 2, 4, 6, 8, 10, 12}`

Some Properties of the Operation of Union :

(i) `A ∪ B = B ∪ A` (Commutative law)

(ii) `( A ∪ B ) ∪ C = A ∪ ( B ∪ C)` (Associative law )

(iii) ` A ∪ φ = A` (Law of identity element, `φ` is the identity of `∪`)

(iv) `A ∪ A = A` (Idempotent law)

(v) `U ∪ A = U` (Law of `U`)

Intersection of sets :

- The intersection of two sets A and B is the set of all those elements which belong to both A and B.The symbol ‘∩’ is used to denote the intersection.
- Symbolically, we write `A ∩ B =` {`x : x ∈ A` and `x ∈ B`}

- The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write `A ∩ B =` {`x : x ∈ A` and `x ∈ B`}.

`A = { 2, 4, 6, 8}` and `B = { 6, 8, 10, 12}`. A ∩ B = { 6, 8 }.

Some Properties of Operation of Intersection :

(i) `A ∩ B = B ∩ A` (Commutative law).

(ii) `( A ∩ B ) ∩ C = A ∩ ( B ∩ C )` (Associative law).

(iii) ` φ ∩ A = φ, U ∩ A = A` (Law of `φ` and `U`).

(iv) `A ∩ A = A` (Idempotent law)

(v) `A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )` (Distributive law ) i. e., `∩` distributes over `∪`(Proof is shown in Fig. )

(v) `A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C )`

This can be seen easily from the following Venn diagrams

Difference of sets (A-B) or (A/B) :

- The difference of the sets A and B in this order is the set of elements which belong to A but not to B.
- Symbolically, we write A – B and read as “ A minus B”

Eg. Let `A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 }`.

`A – B = { 1, 3, 5 }`, since the elements `1, 3, 5` belong to A but not to `B`
and `B – A = { 8 }`, since the element 8 belongs to B and not to A. We note that `A – B ≠ B – A`.

Remark : The sets `A – B, A ∩ B` and `B – A` are mutually disjoint sets, i.e., the intersection of any of
these two sets is the null set as shown in Fig

`"Also note : A-B also represented as A/B"`

Complement of a Set :

- Let U be the universal set and A a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A.
- Symbolically, we write A′ to denote the complement of A with respect to U.

Thus, A′ = {x : x ∈ U and x ∉ A }. Obviously A′ = U – A

E.g. U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}.

A′ = { 2, 4, 6, 8,10 }.

Some Properties of Complement Sets :

(i). `A ∪ A′ = U`
(ii) `A ∩ A′ = φ` (Complement laws)
(iii) `(A ∪ B)´ = A′ ∩ B′`
(iv) `(A ∩ B )′ = A′ ∪ B′` (De Morgan’s law)
(v) `(A′ )′ = A` (Law of double complementation )
(vi). `φ′ = U` and `U′ = φ` (Laws of empty set and universal set)

Important Formula on operation of Sets

1. `A-B = A∩B'`

Proof of this property is shown in Figure with the help of venn diagram

Similarly

2. `A-(B∩C) = (A-B) ∪ (A-C)`
3. `A-(B∪C) = (A-B) ∩ (A-C)`
4.`A∩(B-C) = (A∩B) - (A∩C)`

Formula of union and Intersection :

- If A and B are finite sets, then
` n ( A ∪ B ) = n ( A ) + n ( B ) – n ( A ∩ B )`

- If A ∩ B = φ, then

` n ( A ∪ B ) = n ( A ) + n ( B )`

` n ( A ∪ B) = n ( A – B) + n ( A ∩ B ) + n ( B – A )`

- If A, B and C are finite sets, then

`n ( A ∪ B ∪ C ) = n ( A ) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C )`

`n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) – n [ ( A ∩ B ) ∩ (A ∩ C)]`

Q 2616034870

In a class of `35` students, `24` like to play cricket and `16` like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football ?

Solution:

Let `X` be the set of students who like to play cricket and `Y` be the set of
students who like to play football. Then `X ∪ Y` is the set of students who like to play
at least one game, and `X ∩ Y` is the set of students who like to play both games.

Given ` n ( X) = 24, n ( Y ) = 16, n ( X ∪ Y ) = 35, n (X ∩ Y) =` ?

Using the formula `n ( X ∪ Y ) = n ( X ) + n ( Y ) – n ( X ∩ Y )`, we get

`35 = 24 + 16 – n (X ∩ Y)`

Thus, `n (X ∩ Y) = 5`

i.e., `5` students like to play both games